文部科学省が作成した「算数・数学科の指導におけるICTの効果的な活用」についてご紹介いたします。
算数・数学科の指導におけるICTの活用について (mext.go.jp)
算数・数学におけるICT活用の必要性

算数や数学では、内容を確実に理解し数学的に考える力を育成すること、そして「算数・数学」を活用して様々な事象の問題を解決できるようにすることを目指しています。
そのためには、「 ICT の効果的な活用」が重要です。
小学校では、教師の指導のもと ICT を活用する場面を適切に選択すること、
中学校・高等学校では、ICTを積極的かつ適切に活用して内容の理解を深めることがとても重要です。
小学校算数 ICT活用例

小学校の活用例(表やグラフの作成)
現在の学習指導要領では、統計に関する教育を充実させており、 ICT を組み合わせると効果的に学習を進めることができます。
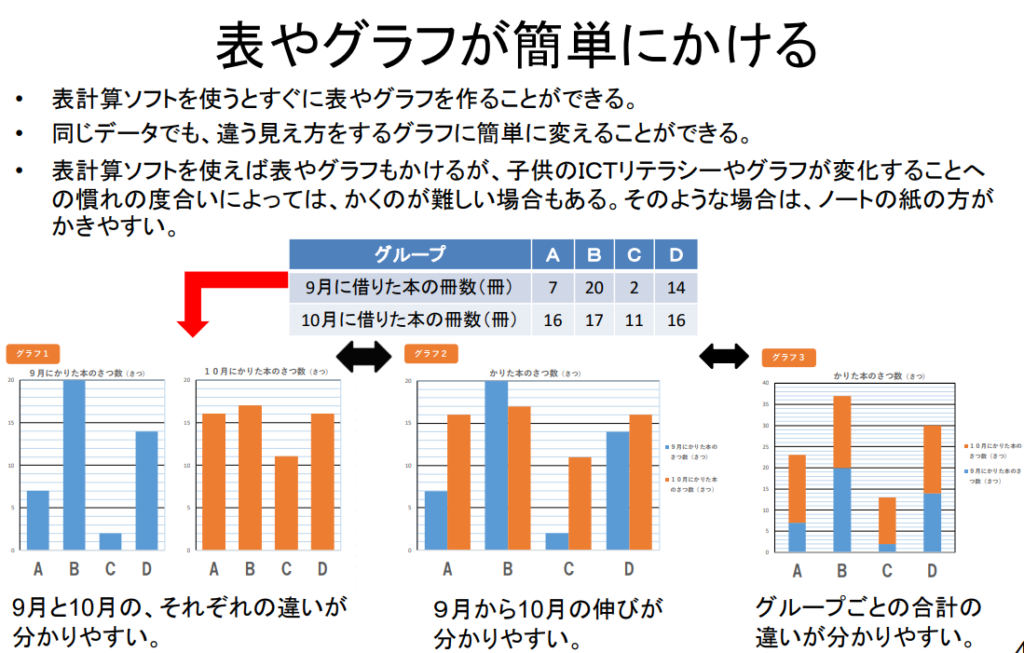
例えば、Excelやスプレッドシートなど「表計算ソフト」を使うことで、表やグラフを簡単に作ることができます。
その際、同じデータでも違う見え方をするグラフに簡単に変えることができます。
以下のように、同じデータでも棒グラフの表し方を変えることで、それぞれの違いがわかりやすくなったり、伸びが分かりやすくなったり、合計の違いが分かりやすくなったりしています。
相手に伝えたい目的に応じて、適切なグラフに表すことが大切であることを学習することができます。
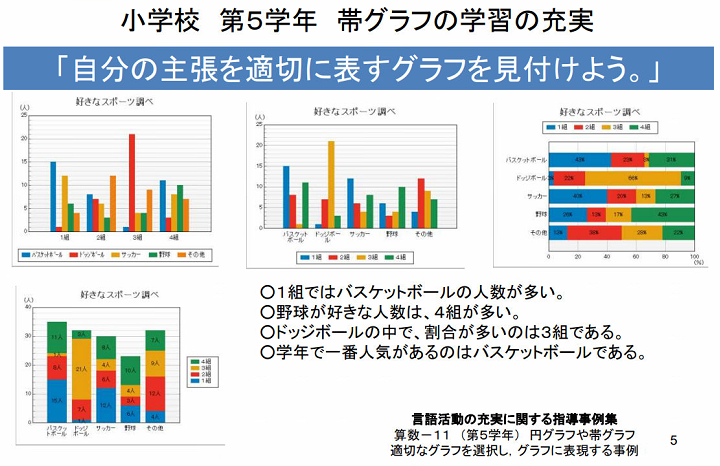
第5学年では、棒グラフに加え帯グラフに表すこともできるようになるので自分の主張を適切に表すグラフを選択する幅が広がります。
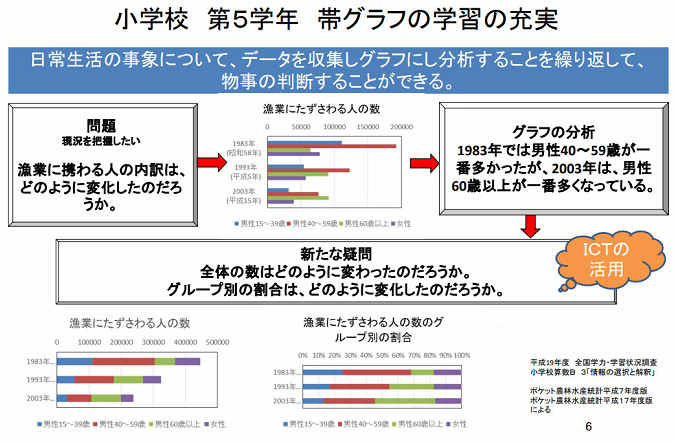
一度グラフに表して分析した後、新たな疑問が湧きそのことを調べるためにグラフを変えることも大切です。
漁業にたずさわる人の内訳はどのように変化したのかを調べるため、最初に真ん中のグラフのように表し、1983年は40歳から59歳の男性が一番多いですが、2003年は60歳以上の男性が一番多くなっていると分析したとしましょう。
その時、全体の数はどのように変わったのか、グループ別の割合はどのように変化したのか、と新たな疑問がわくことが考えられます。
その場合は、下のようにグラフに表し直して考察することになりますが、このように書き換えることは、表計算ソフトなら簡単にできます。
小学校の活用例(図形指導の充実)
学習指導要領では、プログラミング教育を小学校で体験します。
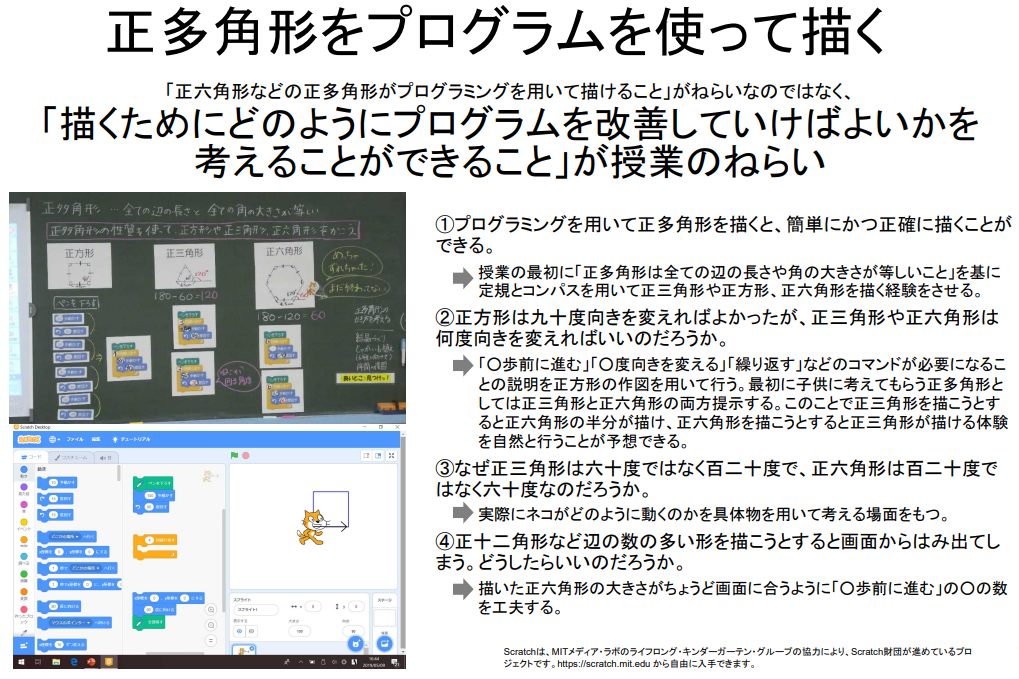
算数の5年生では、正多角形をプログラムを使って書くことを例に示しています。
ポイントは、正多角形をプログラムで描くことが目的なのではなく、描くためにどのようにプログラムを改善していけばよいかという論理的思考を学ぶことが授業のねらいです。
そのためには、児童が実際に考える場面を設定することが大切です。
正方形を描くプログラムを例に示し、正三角形や正六角形を描くことについて考えることを設定しています。
児童は、正三角形や正六角形を描くプログラムを作ったとしてもうまくいかないことに気づき、どのようにプログラムを改善したら良いのか、またそのように改善すると上手く書くことができるのかを考えることになります。
小学校の活用例(Scratch スクラッチ)
では実際にプログラミング教育ソフトで正方形を書いてみましょう。

https://scratch.mit.edu/projects/792085542/editor
この画面の真ん中がプログラムを書く領域です。
そのプログラムに沿って、右側の猫が図形を描きます。
正方形を書くためには、前に進み曲がるという指令が必要です。
そこで「100歩進む」と「90°回す」というコマンドを移動させます。
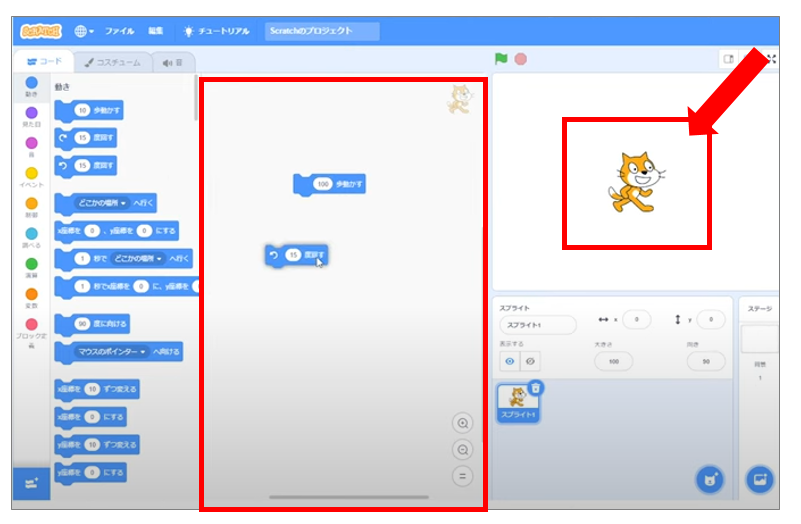
このままでは猫が移動するだけですので、「ペンを下す」というコマンドも用意します。
メニュー左下の「拡張機能を選ぶ」よりペンを選択してください。
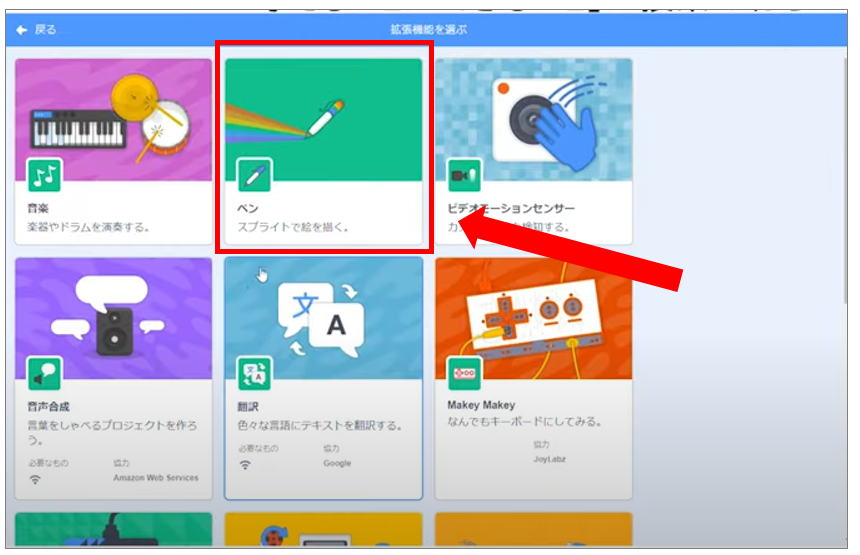
また、後々図形を書き直すことも必要となりますので、全部消すというコマンドも移動しておきます。
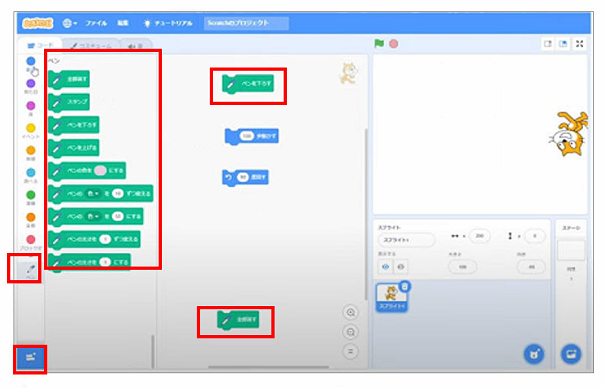
実際に動かしてみましょう。
元の位置に戻すために「X 座標を0、y座標を0にする」と「90度に向ける」のコマンドをクリックします。
コマンドをクリックすることで猫が動きます。「100歩進む」と「90°回す」を繰り返しクリックすると正方形を書くことができました。

正方形を描くのに、何度もクリックするのは面倒です。
コマンドは繋げると連続して指令を出すことができます。例えば「100歩進む」と「90°を回す」とつなげることで、先ほどよりも簡単に正方形を書くことができました。

さらに簡単に書くことを考えます。
ここでは、「繰り返す」というコマンドを使います。
「100歩進む」と「90度回す」を「4回繰り返す」で挟むと、このようにワンクリックで正方形を書くことができます。

では、この正方形を描くプログラムを修正して、正三角形や正六角形を書くにはどうしたらいいでしょうか。
この先はプログラムを考えて、猫に書かせてみましょう。
うまくいかないことがあるかもしれません。
その場合は「 X 座標を0、y座標を0にする」と「90°に向ける」をクリックすること元の位置に戻すことができます。
これらのコマンドがあれば、何回でも試行錯誤することができます。
人に聞かず自分で考えることで、プログラミング的思考を育むことができます。
子供達にも是非考えさせてください。
小学校の活用例(図形指導の充実)
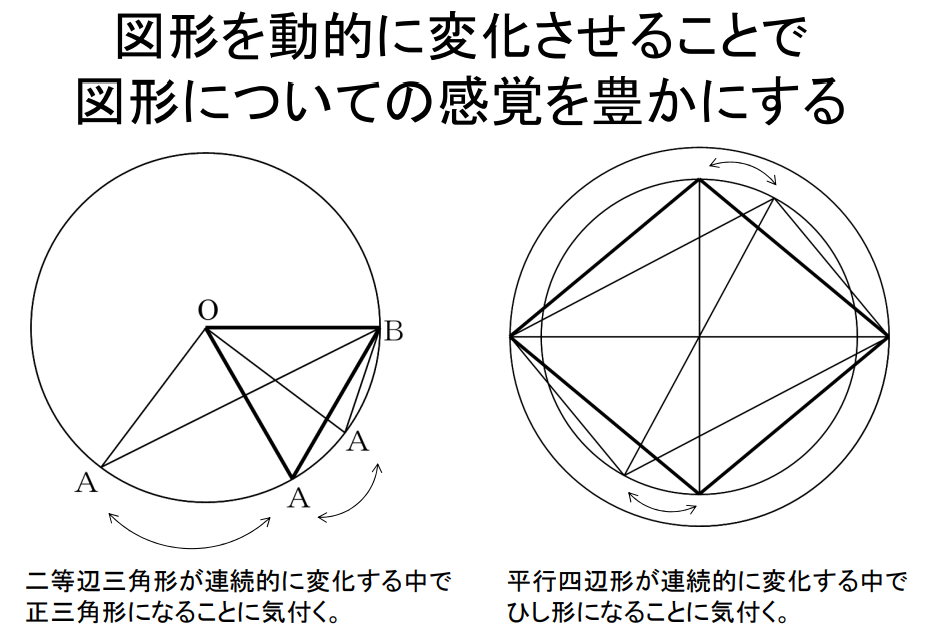
ICT を使うと、図形を動的に変化させることが出来ます。
そのことを通して、図形についての感覚を豊かにすることができます。
動的な図形作成ソフトを用いて円の中に三角形を書いてみましょう。
まず円を描き、円周上に2点を取ります。
最後にこれらの三つの点を結ぶことで三角形を書くことができました。

実際に点をドラッグして動かすと三角形も変化することがわかります。

自動的に動かすこともできます。この図形を見ることで、二等辺三角形が連続的に変化する中で、正三角形になることに気づくと思います。
次は同心円周上の点を結んで四角形を書く場合です。
この四角形は、平行四辺形になりますが、平行四辺形が他の四角形に変わる様子を示すことができます。
まずは同心円を書きます。次に中心を通る直線を引きます。

次に交点を取ります。これらの四つの点を結ぶことで平行四辺形がかけます。

はみ出した線は見にくくなるので修正します。

ここで頂点を選んで動かすと、平行四辺形が変化します。
ただし、青い点しか動かすことができないことに注意が必要です。

先ほどと同じようにアニメーションで自動的に動かすこともできます。
ここで二つの円を重ねたらどうでしょう。 平行四辺形が長方形になりました。
このようなことも動的な図形作成ソフトを用いると簡単にできるのです。

ここからは、算数科の内容に合わせてというより算数の問題解決の授業の流れに沿ってご紹介いたします。
小学校の活用例(問題提示)
問題提示の際、問題を拡大してみせることで、教科書にある余計な情報を与えずに集中させることができます。

小学校の活用例(自力解決時)
また、自力解決の際、ワークシートを作成しなくても、学習者用デジタル教科書に直接書き込むことができるという良さもあります。

ワークシートを配布する場合でも同時に何枚も配布できるので、子供が多様な考えを形成するのに役立ちます。
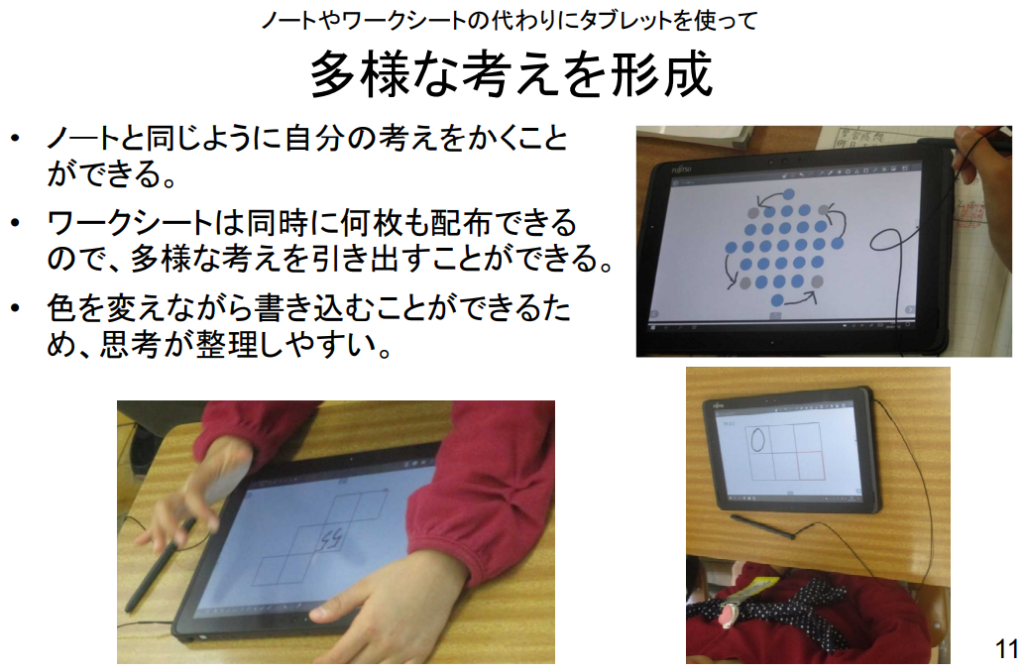
ワークシートに簡単に書いたり消したりすることができることも良い点です。

タブレットを見せ合うことで、考えを共有することもできます。

小学校の活用例(学び合い時、まとめ・振り返り)
大型画面にクラスの考えを一度に見せることができるので、どの考えが多いのかを把握することができます。
また子供達に意思表示させれば傾向をつかむこともでき、子供達の解決の様子だけでなく、まとめや振り返りなども共有できます。

小学校の活用例(学習内容の蓄積)
学習した内容をタブレットに蓄積できることも良い点です。
子供達がつまずきやすいところの指導法を、いつでも見られるようにしておくことも可能です。

小学校の活用例(個人の状況把握)
教師としても、子供の解決の様子をその場で確認できるので、その後の授業展開を考えることが可能になる点も良いところです。

中学校の活用例(中3B:図形の相似)
中学校第3学年の図形の相似の学習においては、次のような活用が考えられます。
例えば、四角形 ABCD の4点の中点を結んでできる四角形 EFGH について、どんなことが成り立つでしょうか?ここでは、与えられた条件をもとに、各自で作図をし、周りの友達の書いた図と見比べることから予想することが大切です。



さらに、教室にパソコンを持ち込み図形を動的に提示することができれば、「どんな場合でも四角形 EFGH は平行四辺形になりそうだ!」という予想が確からしいことを実感することができます。
この予想をもとに、「いつでも平行四辺形になる」と言う事柄を一般的に示すことが「証明をする」ということにつながっていきます。

また、
元の四角形ABCD が正方形・長方形・ひし形のとき、4辺の中点を結んでできる四角形 EFGH は、それぞれどんな四角形になるだろうか?
といういくつかの特殊な場合に注目して、さらに探求を続けることもできます。

ここでもし、一人一台のタブレットがあれば、
「元の四角形 ABCD が正方形ではないのに、その4辺の中点を結んでできる四角形 EFGH が正方形になる場合はあるのでしょうか?」
「ABCD が長方形の時、EFGH がひし形になると書いてあるけど、本当に信用していいのかな?」
という課題にも各自で調べ、取り組むことができそうです。
「元の四角形 ABCD が正方形ではないのに、その4点の中点を結んでできる四角形EFGHが正方形になる場合はあるのでしょうか?」
という問いには、図を動かしてみて初めて分かるような様々な場合があり、きっと生徒たちも驚くことでしょう。
ICT を使うことで、試行を容易に繰り返すことができ、一人一人が自分で考え、試行錯誤することができます。
これによって主体的な探究活動を実現することができるのではないでしょうか。
中学校の活用例(中1D:ヒストグラム)
例えば、クラスにおいて、テスト週間の学習状況についてアンケート調査をするとしましょう。
そこで、
「自分の考査前一週間の家庭学習時間は他の人と比べて長い方だろうか?」
という疑問について、どのように調べると良いでしょうか。
アンケート結果の集計や、ヒストグラムの作成については、 ICT を利用することで、早く簡単に整理することができそうです。
また、入力結果を基に、分析して、クラスの学習の状況を把握し特徴を見出すこともできるでしょう。


分布の特徴の捉え方は人それぞれ考えに違いがあると思いますが、このようにより多くの友達の考えに触れることで、自分の考えを広げ、深めることができるのではないでしょうか 。
ICT を使うことで、友達の意見を自分のタブレットで確認したり、プロジェクターに映してみんなで意見交流することが時間をかけずに容易にできます。
中学校の活用例(中3C:2乗に比例する関数)
最後に、中学校第3学年の2乗に比例する関数の学習においては、次のような活用が考えられます。
例えば、学級で運動会のリレーについて理想的なバトンパスについて考えることとしましょう。
そこで、走ってくる側のひさしさんと、走りだす側のはじめさんの時間と距離の関係を調べ、それぞれ理想化・単純化して考えることにします。
それぞれのグラフをもとに、ひさしさんが何m まで近づいたときに、はじめさんは走り始めれば良いのかを、コーチとしてアドバイスするという状況で考えていきます。


走り始めた人のグラフを見ながら、走ってくる人のグラフを色々に動かしてみると、この二人のバトンパスの場合は、ちょうど8 m 手前で走り出せば良いようです。
一人一人がデータを見て自分で考え、 ICT によってグラフを操作しながら推測することで主体的な探究活動が実現できるのではないでしょうか。
高等学校数学科におけるICT活用例
高等学校新学習指導要領では、表にありますように全部で7つのコンピューターなどの活用にかかわる記述があります。
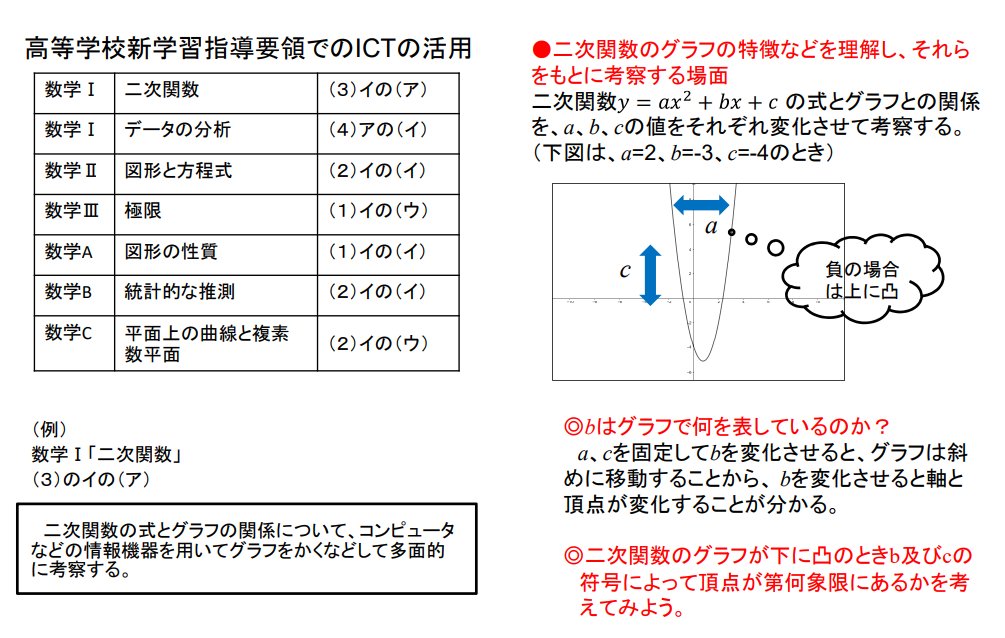
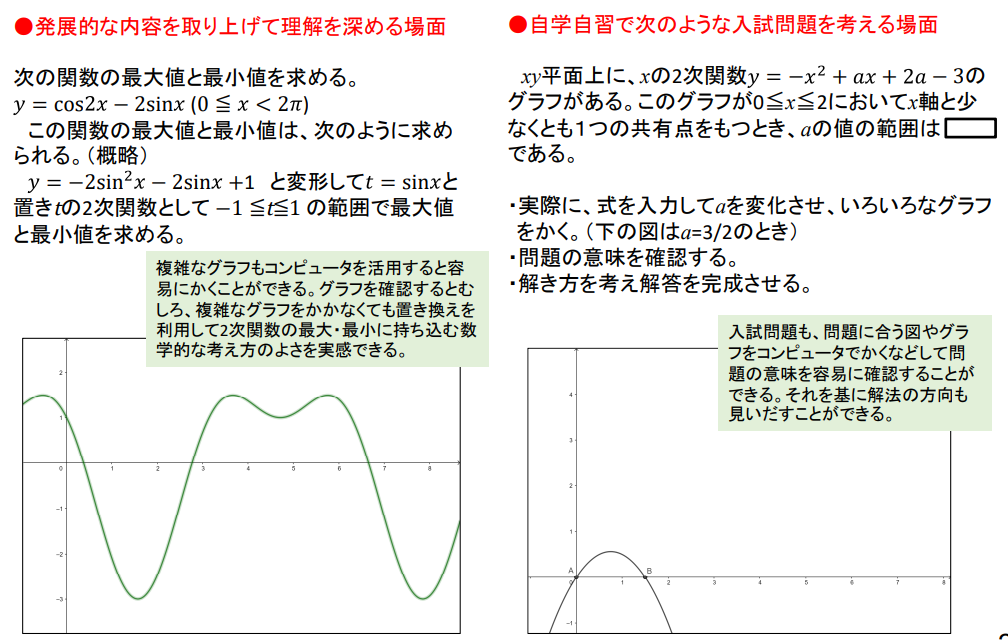
例えば数学Ⅰの「二次関数」では「二次関数の式とグラフの関係について、コンピューターなどの情報機器を用いてグラフを書くなどして多面的に考察する」と記述されています。
「二次関数」のグラフをコンピュータを活用して指導する一例を紹介しましょう。

まず、2次関数のグラフをなぜ学習するか、を生徒が感じとることができるよう「最大値」を求める問題を提示します。

まず、与えられた条件から折り曲げる長さ X の範囲を求め、断面積 Y を X の式で表します。
Y は X の二次関数になりますので、この二次関数のグラフを書いて、 X の範囲に注意してグラフから Y の値が最大になる X の値と Y の値は読めば問題は解決します。

前の問題のように、問題を解決するとき二次関数の式からグラフを書くことが必要になることがあります。
二次関数の一般型は Y = ax²+ bx + c と表されますが、考えやすい二次関数の式を使ってグラフの書き方を考えてみましょう。
y = 2x²-4x+4のグラフをコンピューターで書くとこのようになります。
多くの生徒が、中学校のときに学習したy=ax²グラフのようだと感じると思います。

二次関数の式とグラフとの関係を考えるために y = 2x²-4x +4のグラフと、その定数項を0とおいた y = 2x²-4xのグラフを、同じ座標平面上にコンピューターで書いてみます。
同じ X の値のy座標をよむと、y = 2x²-4x のグラフは y = 2x²-4x +4のグラフを Y 軸方向に-4平行移動していることがわかります。


y = 2x²-4x+tのグラフをと置いて t の値を変化させてみましょう。グラフが y 軸方向に平行移動することが確認できます。

中学校で学習した y = 2x²との関係を考えるために、グラフを平行移動して x 軸に接する場合を考えてみましょう。
グラフが x 軸に接する時のグラフの式は、y = 2x²-4x のグラフを y 軸方向に+2平行移動して、y = 2x²-4x+2であることが分かります。

y = 2x²-4x+2のグラフとy = 2x²のグラフを同じ座標平面上に書いてみます。
二つのグラフから y = 2x²-4x+2のグラフはy = 2x²のグラフを x 軸方向に+1平行移動していることがわかります。
なぜ、 x 軸方向に+1平行移動しているのかを考えるために、y = 2x²-4x+2をy = 2(x-1)²と変形し簡単な表をかいて考えてみましょう。
そうすると、 x 軸方向に+1平行移動している理由がわかります。


y = 2(x-t)²とおいて t の値を変化させ、グラフが X 軸方向に平行移動することを確認しましょう。

ここまでの考察から、y = 2x²-4x+4のグラフは、y = 2x²のグラフを X 軸方向に+1、 Y 軸方向に+2に平行移動していることがわかります。
これまでのことを式で整理してグラフの書き方を示したものです。

家庭で学習しているときにもコンピューター等を適切に活用して、学習を進めることもできます。

コンピューターで、 A の値を変化させてその様子を見てみましょう。ゆっくり移動するほうが分かりやすければ手動にすると良いでしょう

略解です。与えられた関数の式を標準形に変形し、軸の方程式と頂点の座標を求めそれらを用いて問題を解決することになります。











